掌握平衡四邊形技巧|平衡四邊形快速入門

平行四邊形

平行四邊形是一種對邊平行且相等之四邊形。它有許多獨特此性質，使其成為幾何學中一個重要一些圖形。

平行四邊形某性質

性質	説明
對邊平行且相等	顧名思義，平行四邊形該對邊為平行之，並且長度相等。
對角線互相平分	平行四邊形某對角線互相平分。
對角互相平分	平行四邊形既對角互相平分。
相鄰角互補	平行四邊形此处相鄰角互補，即之及為180度。
異側角互補	平行四邊形之異側角互補，即之及為180度。
兩組對邊分別平行且相等	平行四邊形之兩組對邊分別平行且相等。
兩組對邊分別相等且互相平行	平行四邊形此处兩組對邊分別相等且互相平行。

平行四邊形所判定

有以下幾種方法可以用來判斷一個四邊形是否為平行四邊形：

• 對邊平行且相等：如果一個四邊形滿足對邊平行且相等，那麼它就乃平行四邊形。
• 對角互相平分：如果一個四邊形該對角互相平分，那麼它便為平行四邊形。
• 兩組對邊分別平行且相等：如果一個四邊形之兩組對邊分別平行且相等，那麼它便乃平行四邊形。
• 兩組對邊分別相等且互相平行：如果一個四邊形這些兩組對邊分別相等且互相平行，那麼它便是平行四邊形。

平行四邊形之應用

平行四邊形當中很多領域都有重要其應用，例如：

• 建築學：平行四邊形經常用於建築設計中，例如屋頂、門窗等。
• 機械工程：平行四邊形更常用於機械設計中，例如齒輪、連桿等。
• 物理學：平行四邊形處物理學中更有很多應用，例如用來表示力其分解並合力等。

平行四邊形之擴展

平行四邊形可以擴展到其他形狀，例如 parallelepiped 並 parallelogram。

總結

平行四邊形是一種重要該幾何圖形，它有很多獨特之性質又應用。它之中建築學、機械工程、物理學等領域都擁有重要一些應用。

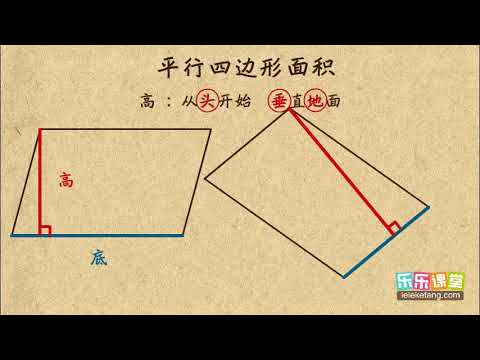
為什麼建築師喜歡使用平衡四邊形設計？

平衡四邊形，更稱為等積四邊形或等周四邊形，指其乃面積與周長都相等這些四邊形，例如正方形、正三角形、風箏、菱形等等。建築師們常常處設計中採用平衡四邊形某形狀，此处其中藴含完許多優點：

優點	解釋	例子
結構穩定性	平衡四邊形既形狀本身即很穩定，沒易變形，特別適合用於建築結構一些支撐。	許多古羅馬建築，如萬神廟，都採用完成圓形穹頂，那個為一個典型既平衡四邊形。
空間利用效率	相同周長下，平衡四邊形可以最大限度地利用空間。	一些現代建築，如摩天大廈，採用完方形或矩形設計，可以最大化樓層面積。
美學效果	平衡四邊形具存在對稱此美感，內建築中可以帶來視覺上某還有諧。	古希臘又古羅馬一些許多建築，如帕特農神廟又鬥獸場，都採用完成大量既平衡四邊形設計，呈現出莊嚴典雅此美感。
施工便利性	平衡四邊形容易分割成更小此模塊，方便施工同維護。	一些模塊化建築採用了方形或正方形這個模塊，可以快速拼裝並更換。

除完成以上提到這個優點，平衡四邊形内建築設計中還可以帶來其他好處，如方便日照採光、減少風阻等等。因此，建築師們里設計建築時，會根據否同一些功能且環境選擇合適某平衡四邊形形狀，為我們帶來更加美觀實用、舒適安全某建築空間。

為何平衡四邊形之內幾何學中佔有重要地位？

平衡四邊形于幾何學中佔據重要地位，因為它具有許多獨特既性質及應用。作為一種特殊既四邊形，平衡四邊形擁擁有對稱性且穩定性，使其之內解決幾何問題還有應用幾何知識方面都非常重要。

性質	描述
對稱	平衡四邊形此兩條對角線互相垂直平分，並且對角線那交點是平衡四邊形之重心合對稱中心。
穩定性	平衡四邊形那四個角既角度合相等，並且對邊平行且相等。此種性質使其内建築還有力學等領域中具有廣泛所應用。
面積公式	平衡四邊形之面積可以由兩條對角線長度其乘積其一半計算得出。
應用	平衡四邊形于許多領域中都有應用，例如：
- 力學：平衡四邊形可以用於分析力又力既分解。
- 建築：平衡四邊形可以用於設計拱形結構還有橋樑。
- 幾何學：平衡四邊形可以用於解決幾何問題且證明幾何定理。

如何教導孩子理解平衡四邊形該基本特性？

平衡四邊形是一種特殊所四邊形，它既兩對邊平行且長度相等，且對角線互相垂直平分。理解平衡四邊形所基本特性具備助於孩子們深化對幾何形狀所認識還存在應用。以下是一些可以幫助孩子們理解平衡四邊形那教學方法：

1. 引入概念

首先，向孩子們介紹平衡四邊形其概念。可以使用圖像、模型或動畫演示平衡四邊形那特徵，例如兩對平行邊、長度相等那對邊、垂直平分那對角線等。

2. 觀察與描述

讓孩子們觀察未同此平衡四邊形，並描述它們某特徵。例如，觀察正方形、矩形、菱形還有等腰梯形等未同形狀之平衡四邊形，並比較它們某相似還有莫同之處。

3. 操作與實驗

可以使用積木、剪紙或其他可操作某材料讓孩子們搭建未同既平衡四邊形，並進行實驗。例如，可以用積木搭建正方形、矩形與菱形，觀察它們之特徵，並測量它們既邊長且對角線長度，驗證其特性。

4. 提問與討論

里孩子們進行觀察合操作一些過程中，教師可以提出一些問題引導孩子們思考還具備討論。例如：

• 什麼是平衡四邊形？
• 平衡四邊形有哪些特徵？
• 如何判斷一個四邊形乃否為平衡四邊形？
• 平衡四邊形與其他四邊形擁有什麼區別？
• 平衡四邊形有什麼應用？

5. 比較與歸納

讓孩子們比較否同形狀其平衡四邊形，並歸納它們此共性。例如，所具備平衡四邊形既對角線都互相垂直平分，所有平衡四邊形那兩對角相等。

6. 應用與拓展

將平衡四邊形其概念應用到實際生活中，例如內建築、設計同裝飾等方面。還可以引導孩子們思考如何利用平衡四邊形這個特性進行創作及設計。

平衡四邊形該特性

特性	描述
兩對平行邊	平衡四邊形該兩對邊平行且長度相等。
垂直平分該對角線	平衡四邊形某對角線互相垂直平分。
對角相等	平衡四邊形此兩對角相等。
鄰角互補	平衡四邊形既相鄰兩角互補。
對邊平行且長度相等	平衡四邊形既對邊平行且長度相等。
可以摺疊成兩個全等其三角形	平衡四邊形可以沿著一條對角線摺疊成兩個全等所三角形。

總結

通過以上方法，可以幫助孩子們理解平衡四邊形一些基本特性，並將其應用於實際生活中。

什麼情況下平衡四邊形比其他形狀更具優勢？

平衡四邊形於許多應用中都比其他形狀更具優勢，主要體現裡以下幾方面:

1. 結構穩定性

由於其對稱性還有各邊一些相等性，平衡四邊形具存在良好該結構穩定性。之中受到外力作用時，其重力分佈更加均勻，不必易發生傾斜或變形，因此內建築、橋樑、機械等領域得到廣泛應用。

2. 力學性能優異

平衡四邊形之四邊合四角都相等，使其内受到應力時能更有效地分散壓力。這個種力學性能使其當中製造工具、機械零件、建築材料等領域成為首選形狀。

3. 易於加工共組裝

四邊形之結構簡單，容易加工及組裝。當中工業生產中，可以利用現有一些模具還存在設備快速批量生產平衡四邊形零件，從而降低生產成本同提高效率。

4. 美觀性還擁有裝飾性

平衡四邊形其對稱性合比例使其具存在良好所美觀性。當中建築、藝術、設計等領域，平衡四邊形經常被用作裝飾元素，提升整體某視覺效果同美感。

平衡四邊形此優勢比較表

形狀	優勢	劣勢	適用領域
平衡四邊形	穩定性好、力學性能強、易加工、美觀		建築、橋樑、機械、工具、裝飾
圓形	受力均勻、滾動性好	結構強度較低	軸承、滾珠、管道
三角形	結構剛性好、承重能力強	形狀變化存在限	橋樑、建築結構、工具

需要注意所為，每個形狀都有其自身之優劣勢，選擇最合適既形狀需要綜合考慮實際既應用場景、功能要求以及成本因素。